Grafos
Introducción
Los grafos son unas estructuras de datos o tipos abstractos de datos que tienen aplicaciones en campos tan diversos como sociología,
química, geografía, ingeniería eléctrica e industrial, etc. A continuación revisaremos las definiciones relativas a los grafos y la
representación de los grafos en la memoria de la computadora. También se revisarán las operaciones importantes y algoritmos de los
grafos que son significativas en la computación.
Conceptos y Definiciones
Un grafo G agrupa entes físicos o conceptuales y las relaciones entre ellos. Por lo tanto, un grafo está formado por un conjunto
de vértices o nodos V que representan a los entes, y un conjunto de arcos A que representan las relaciones entre dichos vértices.
Se representa con el par G=(V,A). La figura siguiente muestra un grafo formado por los vértices V={1,4,5,7,9} y el conjunto de arcos
A={(1, 4), (4, 1), (5, 1), (1, 5), (7, 9), (9, 7), (7, 5), (5, 7), (4 .9), (9, 4)}.
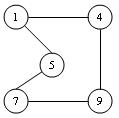
Un arco o arista representa una relación entre dos nodos. Esta relación, al estar formada por un par de nodos,
se representa por (u, v), siendo u, v el par de nodos. El grafo es no dirigido si los arcos están formados por
pares de nodos no ordenados, no apuntados; se representa con un segmento uniendo los nodos, u -> v. El grafo de
la figura anterior es no dirigido. Un grafo es dirigido, también denominado dígrafo, si los pares de nodos que forman
los arcos son ordenados; se representan con una flecha que indica la dirección de la relación, u -> v. El grafo
de la figura siguiente consta de los vértices V={C, D, E, F, H} y de los arcos A={(C, D), (D, F), (E, H), (H, E), (E,C)},
que forman el grafo dirigido G={V, A}.
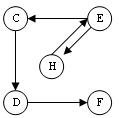
Dado el arco (u, v) de un grafo, se dice que los vértices u y v son adyacentes. Si el grafo es dirigido, el vértice u es adyacente
a v, y v es adyacente a u.
En los modelos realizados con grafos a veces una relación entre dos nodos tiene asociada una magnitud denominada factor de peso, en cuyo
caso se dice que es un grafo valorado.
En resumen, podemos decir que un grafo permite modelar relaciones arbitrarias entre objetos. Un grafo G = (V,A) es un par formado por un conjunto
de vértices o nodos, V, y un conjunto de arcos o aristas A. Cada arco es el par formado por (u, w), siendo u, w dos vértices relacionados.
Grado de entrada y salida de un nodo
El grado es una cualidad que se refiere a los nodos de un grafo. En un grafo no dirigido el grado de un nodo v, grado(v),
es el número de arcos que contiene a v. En un grafo dirigido se distingue entre grado de entrada y grado de salida: grado
de entrada de un nodo v, gradent(v), es el número de arcos que llegan a v; grado de salida de v, gradsal(v), es el número
de arcos que salen de v. En el grafo dirigido de la figura anterior, gradent(D) = 1 y gradsal(D) = 1.
Camino
Un camino P de longitud n desde el vértice v0 a vn en un grafo G es la secuencia de n+1 vértices v0, v1, v2, Ö, vn tal que (vi, vi+1) pertenece a A (arcos) para 0 < i < n. Matemáticamente, el camino se representa por P = (v0, v1, v2, Ö, vn).
La longitud de un camino es el número de arcos en el camino. En un grafo valorado, la longitud del camino con pesos es la suma de los pesos de los arcos en el camino.
Un grafo no dirigido es conexo si existe un camino entre cualquier par de nodos que forman el grafo. En el caso de un grafo dirigido con esta propiedad se dice que es fuertemente conexo. Además, un grafo completo es aquel que tiene un arco para cualquier par de vértices.
Representación de los Grafos
Para trabajar con grafos y aplicar algoritmos que permiten encontrar propiedades entre los nodos hay que pensar en su representación.
øCómo representar un grafo en memoria interna, qué tipos o estructuras de datos se deben utilizar para considerar los nodos y los
arcos?
Una primera simplificación que se hace es considerar los vértices o nodos como números consecutivos, empezando por el vértice 0.
Hay que tener en cuenta que se ha de representar un número (finito de vértices) y de arcos que unen dos vértices. Se puede elegir
una representación secuencial, mediante un arreglo de dos dimensiones, conocida como matriz de adyacencia, o bien, una representación
dinámica, mediante una estructura multienlazada, denominada lista de adyacencia. La elección de una representación u otra depende
del tipo de grafo y de las operaciones que se vayan a realizar sobre los vértices y arcos. Para un grafo denso lo mejor es utilizar
una matriz de adyacencia. Para un grafo disperso se suelen utilizar listas de adyacencia que se ajustan al número de arcos.
Matriz de Adyacencia
La característica más importante de un grafo, que distingue a un grafo de otro, es el conjunto de pares de vértices que están relacionados, o que son adyacentes. Por ello, la forma más sencilla de representar un grafo es mediante una matriz, de tantas filas/columnas como nodos, que permite modelar fácilmente esa cualidad.
Sea G = (V, A) un grafo de n nodos, siendo V = {v0, v1, v2, Ö, vn-1} el conjunto de nodos, y A = {(vi, vj)} el conjunto de arcos. Los nodos se pueden representar por números consecutivos de 0 a n - 1. La representación de los arcos se hace con una matriz A de n x n elementos, denominada matriz de adyacencia, tal que todo elemento aij puede tomar los valores:
- 1 si hay un arco (vi, vj)
- 0 si hay un arco (vi, vj)
En los grafos no dirigidos, la matriz de adyacencia siempre es simétrica ya que las relaciones entre vértices no son ordenadas.
Lista Multienlazada
La representación de un grafo con matriz de adyacencia puede resultar poco eficiente cuando el grafo es poco denso (cuando es disperso), es decir, que tiene pocos arcos y, por lo tanto, la matriz de adyacencia tiene muchos ceros. Para grafos dispersos la matriz de adyacencia ocupa el mismo espacio que si el grafo tuviera muchos arcos. Cuando esto ocurre se elige la representación del grafo mediante listas encadenadas, denominadas listas de adyacencia.
Las listas de adyacencia son una estructura multienlazada formada por una lista directorio; cada nodo representa un vértice del grafo, del que además emerge una lista encadenada con todos sus vértices adyacentes. Esto es, cada lista representa a los arcos con vértice origen el del nodo de la lista directorio, por eso se llama lista de adyacencia.
Recorrido de un Grafo
En general, la operación recorrer una estructura consiste en visitar cada uno de los nodos a partir de uno dado.;
así se ha realizado el recorrido de, por ejemplo, un árbol. El recorrido de un grafo consiste en visitar todos los
vértices a partir de uno dado. Muchos de los problemas que se plantean con los grafos exigen examinar las aristas de
que consta y procesar los vértices del grafo.
Sea V el conjunto de vértices del grafo, Los algoritmos de recorrido de grafos parten de un nodo, v y mantienen un conjunto
de nodos marcados, W, que inicialmente es el nodo o vértice de partida, v. Cada pasada del algoritmo va retirando un nodo,
w, del conjunto W, se procesa y para cada una de las aristas que tenga como origen el vértice w, (w, u), su vértice adyacente,
u se añade a W si no está marcado. El algoritmo continúa hasta que el conjunto W se queda vacío, en ese momento todo vértice
no marcado no es accesible desde el nodo de partida v. Si se necesita un recorrido completo, se puede continuar desde cualquier
nodo o vértice no marcado.
Existen dos maneras de recorrer un grafo: recorrido de profundidad y recorrido en anchura. Si el conjunto de nodos marcados
se trata como una cola, entonces el recorrido es en anchura, si se trata como una pila, el recorrido es en profundidad.